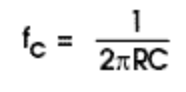揭秘合成器(6):频率响应与共振
- 作者:Gordon Reid
- 编译:Rejor(@Evilsine)
- 出处:Sound On Sound
在本系列的第四与第五篇文章中,我们了解了即便是最简单的模拟滤波器也会使声音发生复杂的变化。本文将介绍更加复杂的滤波器设计将会对声音产生什么样的影响。
如果你有阅读本系列的前两篇文章(点击这里查看《揭秘合成器(4):滤波器与相位》和《揭秘合成器(5):深入滤波器》),你应该会了解如何(至少在理论上)制造一个 24dB/oct 滤波器以及如何定义其截止频率。你还应该了解该滤波器将会对通过的信号的相位及谐波成分造成怎样的影响。所以现在我们要开始讨论如何把共振调到 11 点位置,给输入信号添加失真,实现经典的模拟滤波器刺耳的扫频效果了吗?
并不是。直到现在,我们讨论的还仅仅只是静态滤波,就像音响的音色控制一样。无论你如何使用静态滤波器,得到的也只能是死气沉沉的音色。本文我们将介绍几种可以给滤波器增添生机的技巧。
1) 截止频率的变换
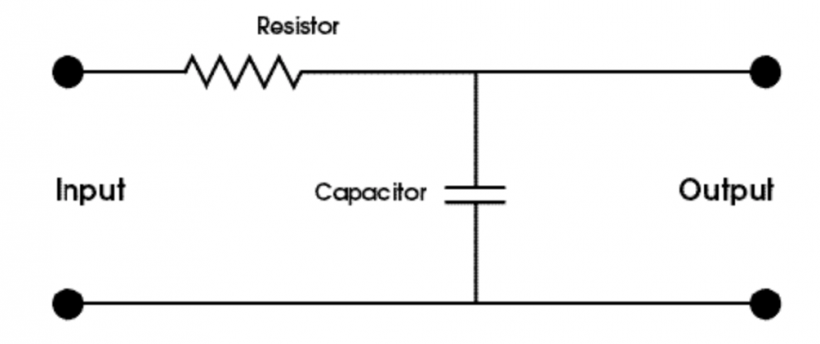
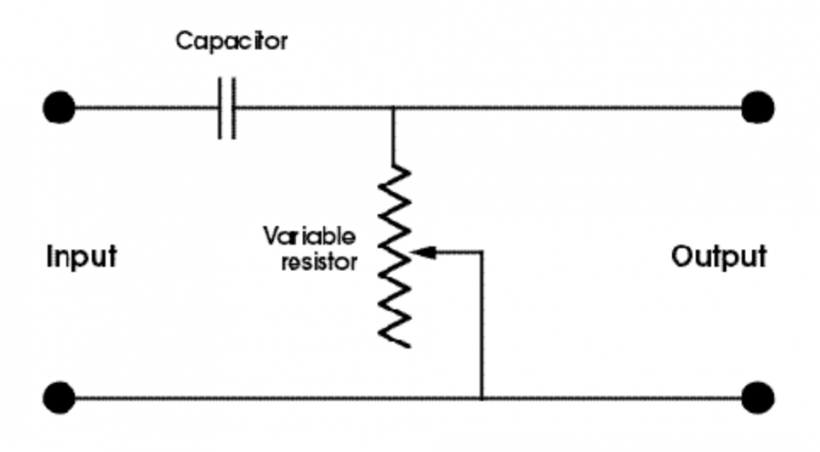
一如既往,我们将从简单的 6dB/octave 低通 RC 滤波器开始讲起(图 1)。
想想看如果我们将图中上方的定格电阻器变换成可变式电阻(又称分压器或电位器)的话将会发生什么。经过上述改变,我们会得到图 2 中的电路。
我将尽量不在本文中引入太多的数学运算,但关于这一滤波器,你需要知道它的一个极其重要的特性:其截止频率与电阻器和电容器的数值直接相关。它们之间具有一个十分简单的关系,可以用下方的算式概括:
换句话说,如果你增加电阻器的数值,截止频率将随之降低。相反地,如果电阻降低,截止频率将随之升高。模拟合成器允许你通过旋钮或者滑杆来控制滤波器的电阻值,从而控制其截止频率。当然,我们这里介绍的是被动滤波器,几乎所有模拟合成器使用的都是主动滤波器(也就是说它们的电路中包含某种形式的信号放大器)。但不管主动被动,其背后的原理是一致的:通过对特定滤波器电路中的一个或多个元件的属性进行调整,从而实现对截止频率的变更。
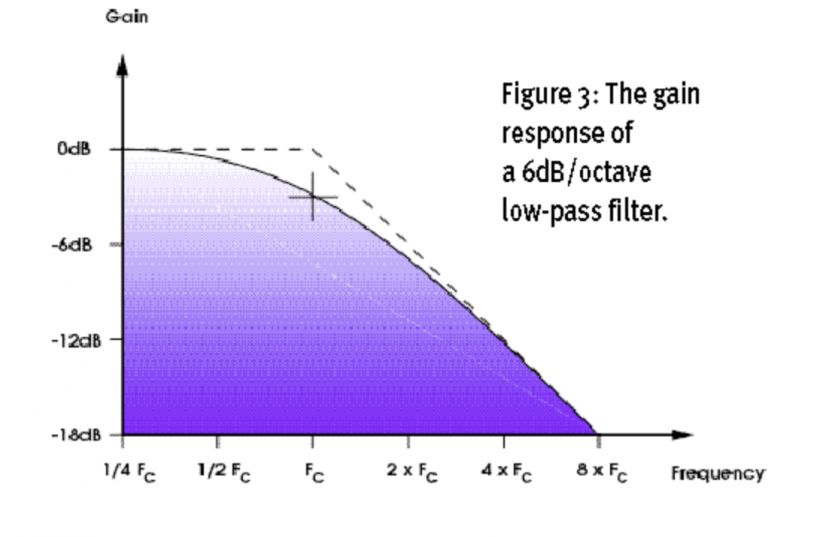
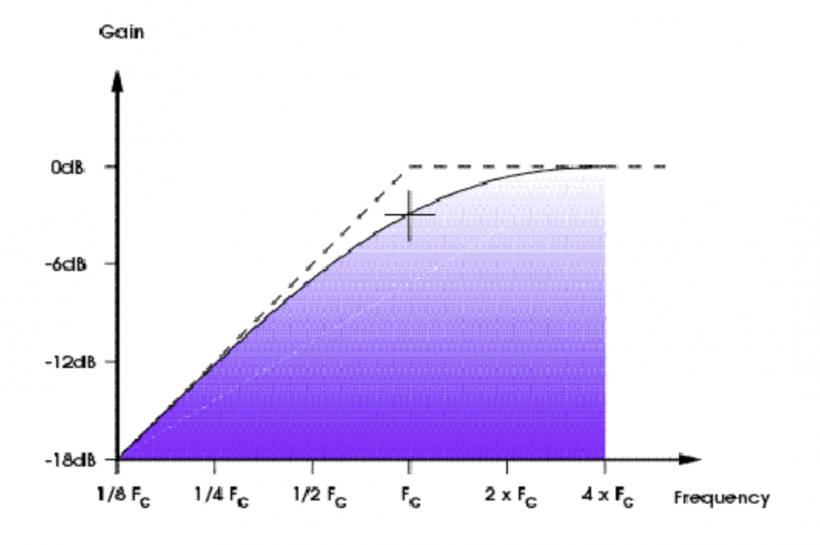
高通滤波器的原理也与此相同。高通滤波器削弱的不是高频谐波,而是低频谐波。图 3 与图 4 展示的是低通与高通滤波器的不同的频率响应。
如图 5 所示,高频滤波器使用的两个电子元件与可变式低通滤波器完全相同,只不过电路中的电容和电阻调换了位置。同样的,截止频率与 1/R 成比例关系。
2) 更多滤波器类型
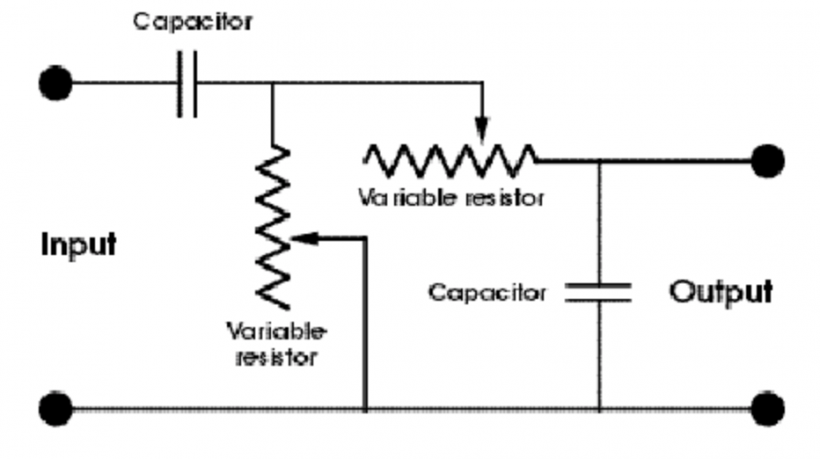
现在请各位发动想象力。如果我们将低通滤波器与高通滤波器组合起来,应该不难得到另一种许多合成器上常用的滤波器:带通滤波器。带通滤波器并不只是将频谱任意一端的频率进行削减,它同时削减两端的谐波,只允许频谱中的一带频率(相对来说)不受削减地自由通过。带通滤波器在概念上十分简单:只需将低通与高通滤波器串联组合即可。经过这一处理我们可以得到图 6 中的电路,其频率响应如图 7 所示。
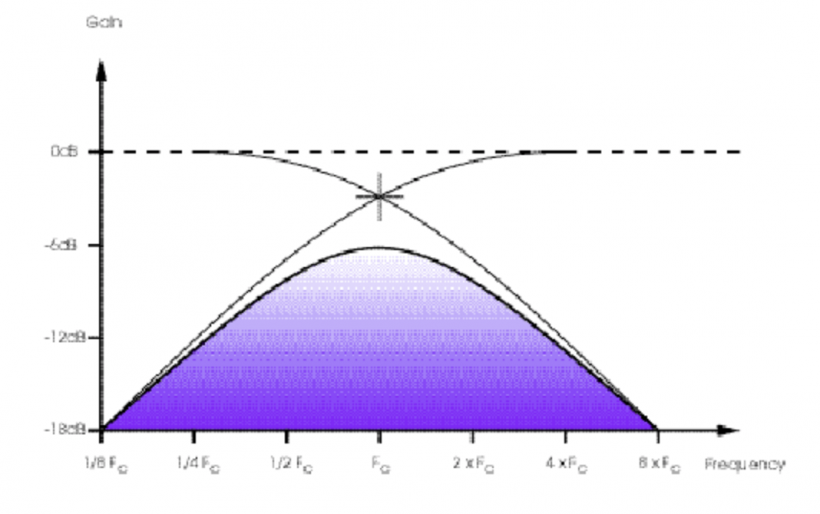
当然,现实情况远远不止这么简单。这样做得到的带通滤波器存在两个问题:第一,正如我们在上一篇文章中讨论过,简单将两个 RC 滤波器进行叠加往往并不能得到理想的效果。第二,如果高通与低通滤波器截止频率相同,信号的整个频谱将会受到衰减,即使在信号最高的位置也会有 6dB 的衰减,其他位置将会衰减更多。这将使信号音量过低,难以进行其他处理。
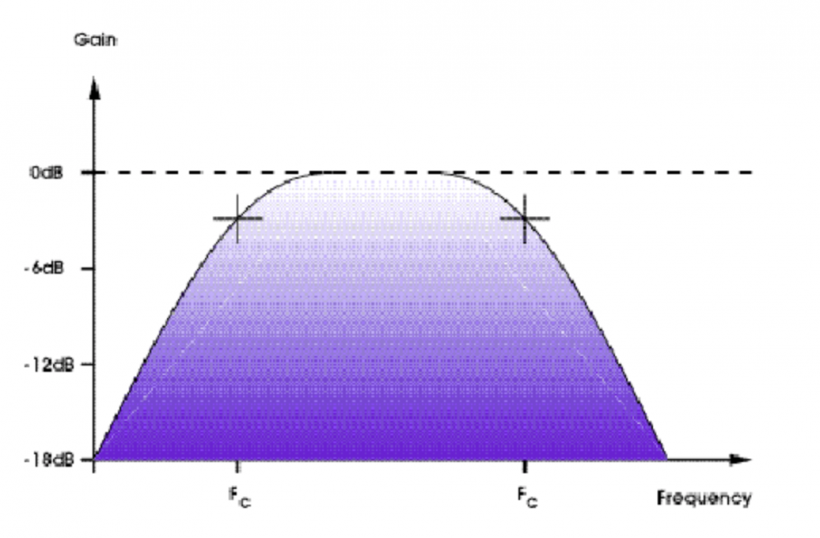
幸运的是,电路设计师可以很简单地克服上述问题。第一种解决方案需要将输入与输出阻抗设计成分割彼此重叠阶段的样式。第二种方案是将两个滤波器的截止频率分离,然后通过将两个滤波器的响应数值提高至 12dB/oct 甚至 24dB/oct 以增添其斜度。经过这样处理的滤波器将会得到与图 8 类似的响应曲线。
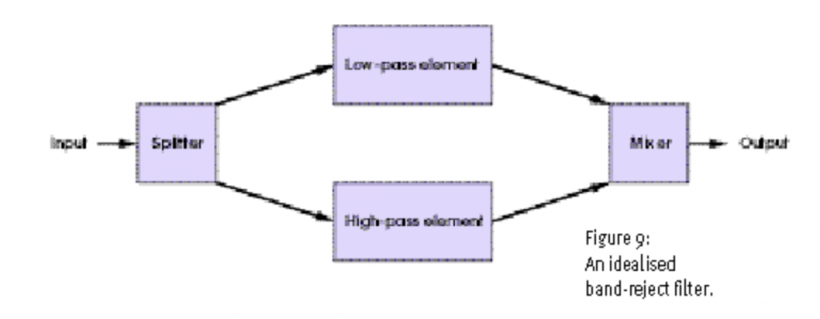
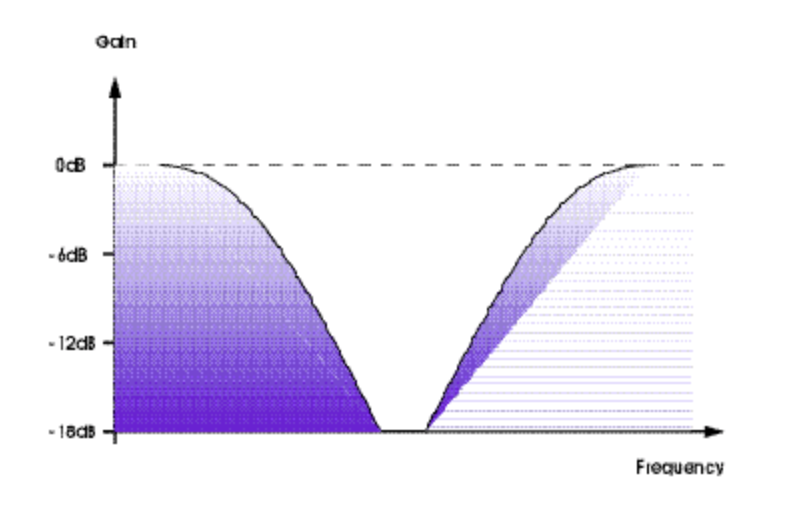
将上述原理进一步延伸,我们可以使用类似的手法创造一个「带阻」滤波器。让我们先拿一个截止频率 1kHz 的低通滤波器,向其输入一个信号。然后将同样的信号输入至平行电路中的 5kHz 的高通滤波器。接着将两条经过处理的信号叠加起来,得到的结果是原始信号的 1kHz 与 5kHz 将几乎原封不动,但 1kHz 与 5kHz 中间的频率将会被削减。听上去没问题,对吧?唔,其实并不是。实际情况下两个单独的滤波器将会为两条信号引入不同的相位偏移,在将两条信号混合的时候,这样的相位偏移将会造成各种音频副作用。不过我们今天暂时不考虑这些问题,理想情况下带阻滤波器及其响应如图 9 与 图 10 所示。
3) 滤波器扫频
所以,经过上面的长篇大论,我们终于要制作各位等候多时的有趣的滤波器扫频声了吗?不好意思,还请再等等。到这里为止我们讨论了你会在传统模拟合成器上见到的各种类型的滤波器:低通、高通、带通和带阻以及梳状滤波器。我们甚至研究了怎样调节其衰减速率以及截止频率。但仍然有两个十分重要的因素需要我们讨论。
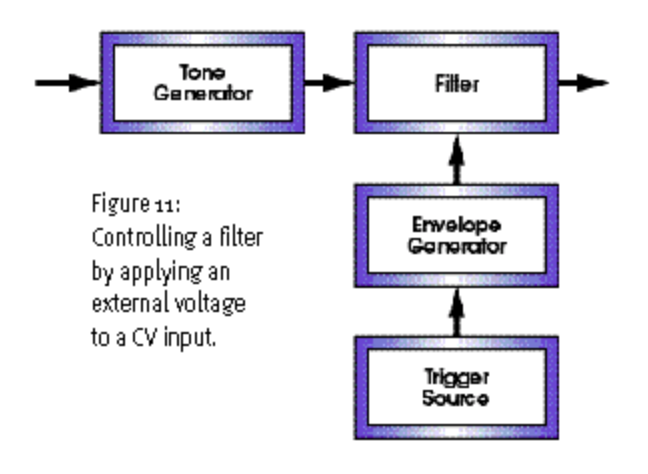
第一个因素非常简单:「电压控制」。如果你回过头阅读本系列的第三篇文章,你会发现一整篇文章都在讨论使用非人为介入的手段对声音进行变换。很显然,你可以将图 2、图 5 以及图 6 中的电位器替换成对外部电压产生响应的装置。这样我们即可使用包络生成器或 LFO 等调制器来制造滤波器扫频效果,见图 11。
第二个重要因素又是什么呢?唔,第二个因素说起来就复杂了…
4) 共振
自然界中的所有物体,几乎无一例外都具有共振。换句话说,几乎所有物体都会在特定频率下自然震动。对于紧绷的琴弦来说,当其被拨动时,其最低的震动频率就是就是它的基频音高。但如果你不碰琴弦的话呢?
想象在一个正在播放音乐的扬声器前面摆放一条琴弦。观察这条琴弦,你会发现有时候该琴弦会随音乐震动,但又有时候它却处于静止状态。这一现象就是共振。如果音乐中的频率与琴弦的共振频率一致,琴弦就会随着音乐产生震动,即共振。如果音乐中不含任何琴弦的共振频率,则琴弦则会保持静止。不光是上述的琴弦,提琴的琴体、管乐器中的空气等等物体均具有共振的性质。实际上,乐器共振频率的位置与共振频率彼此间的关系对于乐器的音色具有决定性的作用。桥梁建筑师在设计吊桥时要保证桥梁不会在风中产生共振。但这又和模拟合成器有什么关系呢?
某些情况下,可以说共振与模拟合成器完全无关。被动 RC 滤波器并没有共振频率。你可以将任何信号输入至被动 RC 滤波器中,不管该滤波器电路有多复杂,它只会让信号原封不动地通过或者根据其响应对信号进行削减。
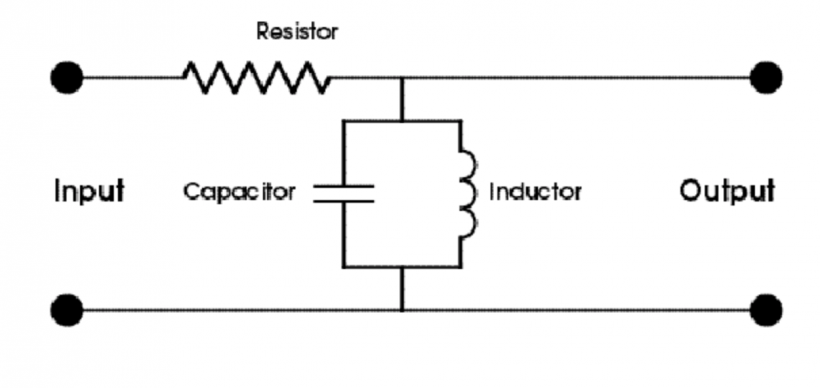
但在另外一些情况下,共振又与合成器又息息相关。如果你将电容器和电阻器与一个叫做「电感器」的元件结合,或者将它们用在两个或更多电极的主动电路中,你将得到一个在某一特定频率拥有巨大峰值响应的电路(见图 12)。
经过被动滤波器处理之后的信号强度往往会被削减,但主动共振电路会对特定频率进行放大,经过处理的信号中,位于这些位置的谐波反而要比原始信号更响。我很希望能够告诉你这一现象为什么会产生,但其背后的数学原理过于复杂,我只能说,位于截止频率附近的谐波将会被主动共振滤波器放大。
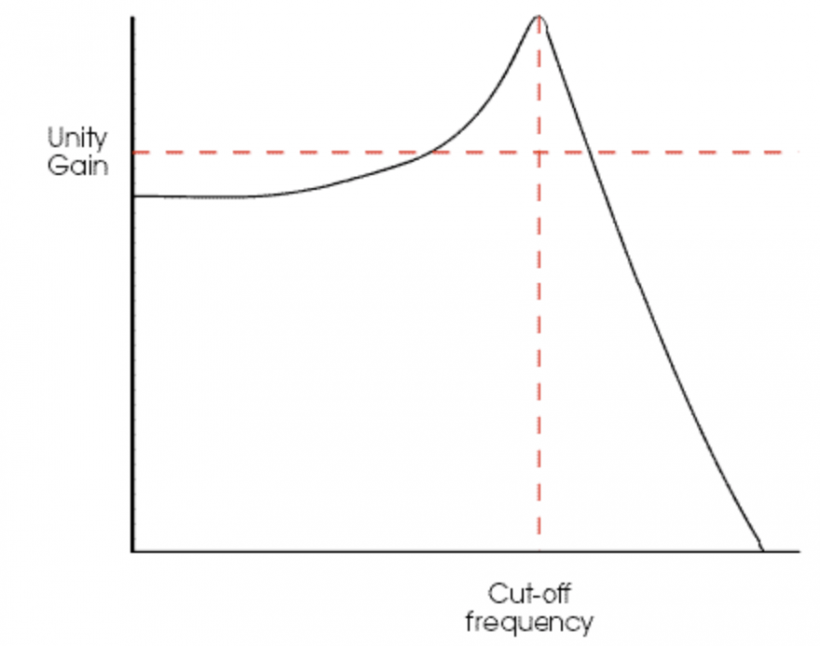
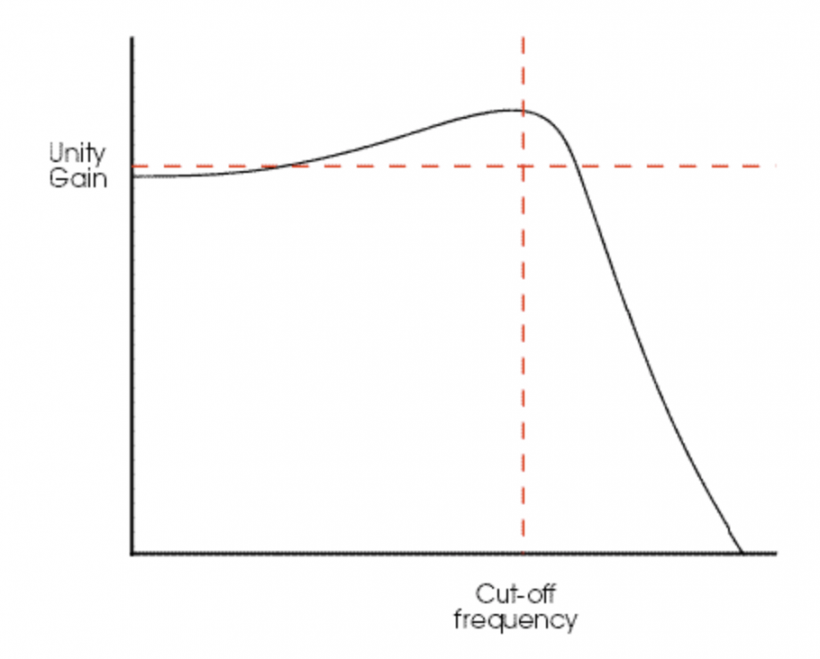
图 13 展示的是一个低通共振滤波器在理想状态下的频率响应。如图所示,该滤波器仍会削减高于截止频率的谐波,但位于截止频率附近的一带谐波反而会被放大。另外,低于截止频率的谐波也多多少少会被减弱。共振峰的宽度由叫做「Q 值」的参数决定,Q 值越低,共振峰会越宽,随着 Q 值升高,滤波器的共振峰将越来越明显,并对信号造成明显的变化。参见图 14 与 图 15。
如果使用电压控制器对截止频率进行调制,使其在频谱中上下运动,其放大的谐波频率也会随之上下扫动。这也就是或许是模拟合成器史上最经典的扫频音色的制作原理。
5) 自共振
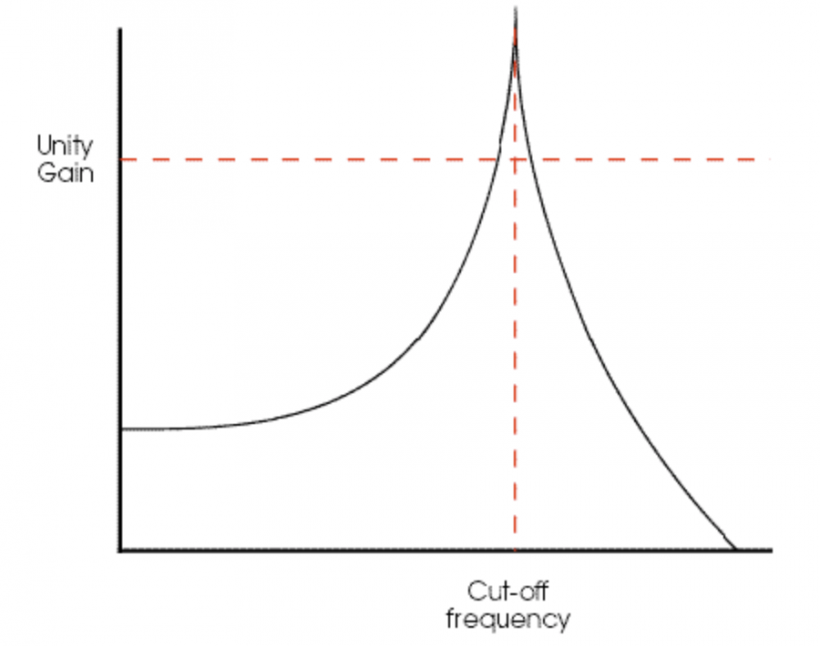
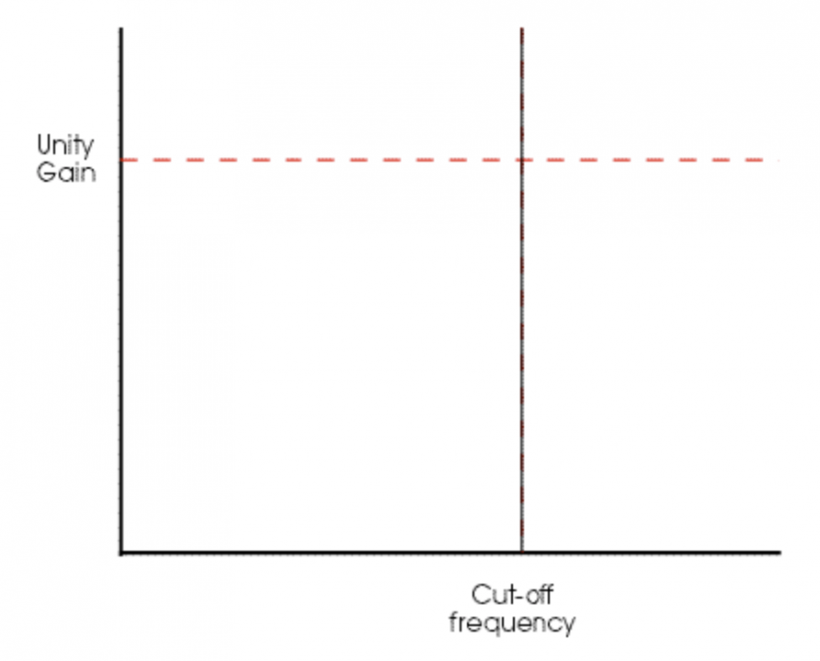
但我们的故事还远没有结束。如果你不断增添 Q 值,共振频率会达到一个极其显著的状态,以至于位于截止频率之下和之上的频率将从信号中消失,并造成另外一些音频效果:滤波器在其截止频率位置开始自我震荡(见图 16)。滤波器自共振会产生十分强大的音频效果,位于自共振边缘的滤波器将会制造出电子合成器特有的非自然音色。
6) 滤波器的创意运用
低通共振滤波器对与减法合成的音色塑造起着至关重要的作用。事实上,因为只对滤波器进行调节就可以对音色造成显著的影响,许多合成器演奏者甚至无视合成器的许多其他参数。本文的剩余部分我们将对滤波器的用法与技巧进行简单讨论,关于滤波器的更多知识,我们会在今后的文章中进一步延伸。
- 你可以使用静态滤波器来强调特定频率,以便为声音赋予一定的个性或者使其在混音中突出。
- 你可以使用两个或多个静态滤波器为音色创建共振波,通过调整这些滤波器的参数,你可以模拟人类的嗓音或者其他传统乐器的声音。
- 如果使用高 Q 值的共振滤波器并使其截止频率追踪音符的音高,你可以创造经典的「强调音」特性,并且无论你在键盘上演奏什么音符,该特性都将保持一致。
- 继续增高 Q 值,可以使滤波器处于自共振的边缘(许多合成器都可以实现这一效果,但有部分合成器不行)。输入信号中的特定频率将会被放大。这一特性可以被用来创建独特的失真效果,十分适合用来制作古怪的声音。
- 将 Q 值调至最大,滤波器将会变成一个正弦波生成器。如果滤波器能够准确追踪键盘 CV,那么你可以通过键盘将滤波器当作额外的振荡器进行演奏。你甚至可以使用滤波器调制 CV 对其添加颤音效果。理论上,处于自共振状态下的滤波器会完全将原始信号移除,但实际上大多数滤波器都允许部分信号在自共振时通过,这样的结果是你将得到现代音乐中经常使用的尖锐音色。
如果你并不熟悉上述滤波器技巧,别担心,我会在今后的文章中详细介绍它们。之所以在本文中提到上述技巧是因为我想让你了解滤波器可以使音频信号产生多么巨大的变化。而且,别忘了刚才提到的所有技巧都只是使用低通滤波器,同样的原理可以适用于高通滤波器、梳状滤波器以及带通及带阻滤波器中。
所以本文的知识对我们音乐人意味着什么?你可以这样想:一个强大的模拟合成器通常会具备多个滤波器。其中大多数将会是主动滤波器,除了无所不在的低通滤波器之外,许多合成器允许你自由选择与组合另外四种滤波器类型。这些滤波器的大多数将支持电压控制,允许你使用各种调制器对截止频率进行调制。许多滤波器还支持共振,给你更多方式对信号进行修整与塑造。部分合成器还允许你调整滤波器的频率衰减斜度,并且支持自共振,以便创造更广泛的声音,甚至允许你将滤波器作为额外的振荡器使用。更高端的滤波器还允许你通过 CV 对 Q 值进行调节,以便制造压控共振音色。一小部分合成器甚至允许你将外部信号插入至反馈循环中来制造共振效果,从而帮助你得到更有趣的音色。
现在你应该知道滤波器对于模拟合成器来说是多么重要了。事实上如果你将一个 Moog 合成器的音色输入至 Korg 滤波器中,得到的声音听起来将与 Korg 合成器十分相似。相反,如果你将 Korg 合成器的波形使用 Moog 滤波器处理,得到的声音就像是你在演奏 Moog 合成器。你或许已经听厌了合成器发烧友整天喋喋不休地讨论各种滤波器,但这些人确实有他们的道理。滤波器对于合成器音色来说至关重要,你的音色将大幅取决于你使用什么滤波器,以及你如何使用它们。这也是合成器世界中众所周知的秘密。
文章出处 https://www.soundonsound.com/techniques/synth-secrets-all-63-parts-sound-on-sound
转载文章请注明出自 Midifan.com
-
2021-06-27
 NeonSounds
顶一下
NeonSounds
顶一下